UP | HOME

Date: [2020-08-30 Sun]

Introduction to Maxima

Table of Contents

Presentation by: Bibek Panthi

< Collapse code block> Expand code block 
(defun bp/copy-source-block () 
  (interactive)
  (save-excursion 
    (org-edit-src-code)
    (kill-ring-save (point-min) (point-max))
    (org-edit-src-abort)))
    
(local-set-key (kbd "M-c") 'bp/copy-source-block)

1. Abacus / History of Computers

  • Computers started with the need for caluclating/computing
  • The First computer
    • additions, subtractions
    • and with some effort multiplication

abacus.jpg

Figure 1: Abacus

2. Modern Calculator

  • division, square roots, and powers
  • Matrix
  • Vectors
  • Statistics
  • and much more

20200907135227-calculator.png

Figure 2: TI-84 Plus

3. But maths is not all about numbers

Arithmetics
Numbers
_Algebra
Symbols_
Geometry
Shapes

4. Computer Algebra System (CAS)

is any mathematical software which manipulates mathematical expressions in a way similar to humans.

  • i.e. just as calcuators do arithmetics, CAS do algebra

5. Maxima

Maxima is a free and open source CAS.

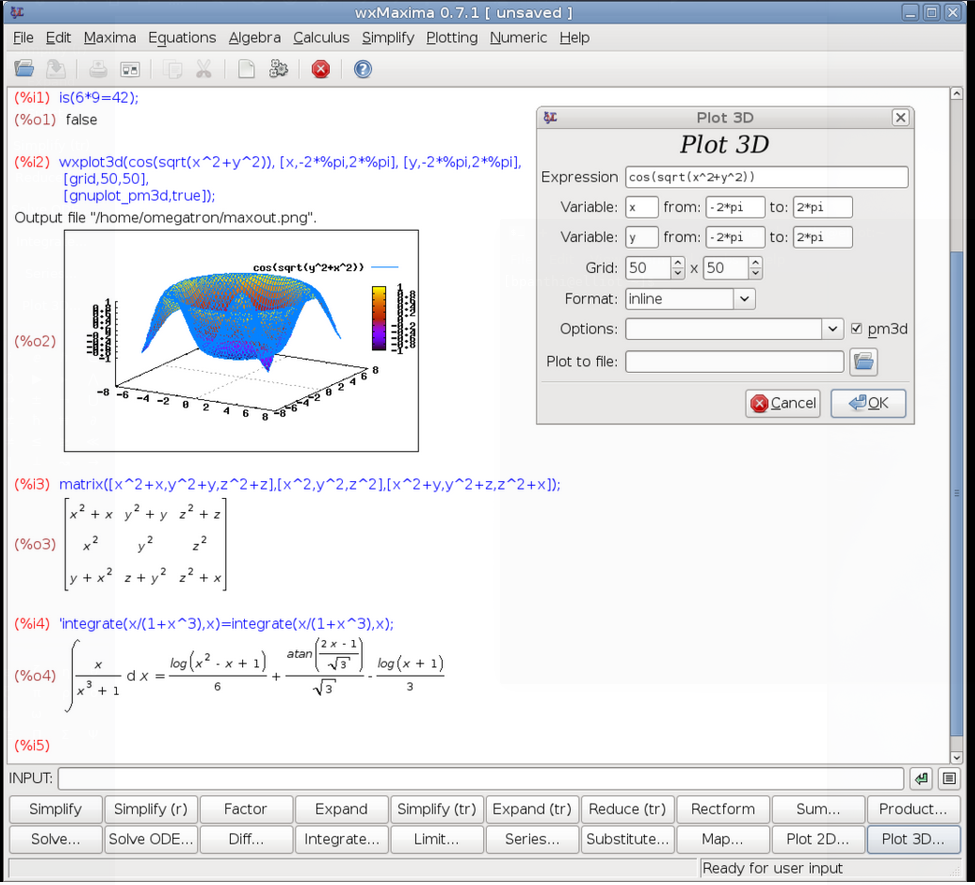
20200907142106-maxima.png

Figure 3: Maxima

6. Example 1

< Collapse code block> Expand code block 
print(1+1);
print(15*15 + 0.5* ( 12/3));
2
227.0
< Collapse code block> Expand code block 
tex(2*x+5*x);
tex(expand((y+x)^2));

\[7\,x\] \[y^2+2\,x\,y+x^2\]

  • Familiar rules of BODMAS

Notice:

  • explicit multiplication
  • %

7. Variables and Expression

  • Assigning values
< Collapse code block> Expand code block 
a:5;
a+1;
  • Evaluating expression with specific values
< Collapse code block> Expand code block 
y: 4*a*(x-1);
print(tex((y, a:2)));

\[2\]

8. Solving Equation

In calculators we could solve:

< Collapse code block> Expand code block 
eqn: x^2 + 4*x + 4 = 0;
print(solve(eqn,x));

[x = - 2]

Now we can handle:

< Collapse code block> Expand code block 
eqn:  a^2*x^2 + 2*a*x + c = 0;
tex(solve(eqn,x));

\[\left[ x=-\left({{\sqrt{1-c}+1}\over{a}}\right) , x={{\sqrt{1-c}-1 }\over{a}} \right] \]

solve can find analytical solutions of:

  • algebraic equations
    • especially polynomial
  • trigonometric equations
  • system of linear and non-linear equations
    • solve for x,y
< Collapse code block> Expand code block 
soln: solve ([y=x, y=4*a*x^2],[x,y]);
tex((soln, a:1/8));

\[{{1}\over{8}}\]

9. Plotting

< Collapse code block> Expand code block 
plot2d ([x, 4*a*x^2],[x,-4,4]),a=1/8;

10. However sometimes analytical solutions don't exist

10.1. Numerical solution

  • find_roots
< Collapse code block> Expand code block 
exp : x^(2/3) + x^(1/2) - 1;
solve(exp, x);
print(find_root(exp, 0, 100));

0.3021706154056545
  • newton
  • mnewton (for multiple nonlinear equations)

11. Simplification

11.1. Rational Simplification

ratsimp()

< Collapse code block> Expand code block 
expr: x+x^2+2*x * (x - 1);
tex(ratsimp(expr));

\[3\,x^2-x\]

< Collapse code block> Expand code block 
expr: (x^(a/2) + 1)^2*(x^(a/2) - 1)^2/(x^a - 1);
tex(ratsimp(expr));

\[{{x^{2\,a}-2\,x^{a}+1}\over{x^{a}-1}}\]

ratsimp (%) fullratsimp (%)

12. Trignometric Simplification

trigsimp()

< Collapse code block> Expand code block 
print(trigsimp(sin(x)^2 + cos(x)^2)); 

1

13. Getting Help

  • example(factor)
  • ? factor
< Collapse code block> Expand code block 
expr: x^2 - 1;
tex(factor(expr));

\[\left(x-1\right)\,\left(x+1\right)\]

14. Constants

  • %pi
  • %e
  • %i
< Collapse code block> Expand code block 
expr: %e^(%pi * %i) + 1;
print(expr);

0

15. Calculus

15.1. limit

< Collapse code block> Expand code block 
expr: 'limit((1 + 5/x) ^ x, x, inf);
tex(expr);
tex(ev(expr, nouns));

\[\lim_{x\rightarrow \infty }{\left({{5}\over{x}}+1\right)^{x}}\] \[e^5\]

< Collapse code block> Expand code block 
expr: 'limit(sin(x)/x*%e^x/x!, x , 0 );
tex(expr);
tex(ev(expr, nouns));

\[\lim_{x\rightarrow 0}{{{e^{x}\,\sin x}\over{x\,x!}}}\] \[1\]

16. Derivative and Integrals

16.1. diff

< Collapse code block> Expand code block 
tex(diff(sec(x)*x^2, x, 2));

\[x^2\,\sec x\,\tan ^2x+4\,x\,\sec x\,\tan x+x^2\,\sec ^3x+2\,\sec x\]

Simplify the result: 

%,x:1;
float(%)

16.2. integrate

< Collapse code block> Expand code block 
tex(integrate(sec(x), x));

\[\log \left(\tan x+\sec x\right)\]

17. Differential Equation

17.1. ode2(y'' + 2y' + y = 0)

Ordinary Differential Equation y'' + 2y' + y =0

18. Example: Projectile motion

< Collapse code block> Expand code block 
ode2('diff(y,t,2) = -g, y, t);

ic2(%o96, t = 0, y = 0, 'diff(y,t) = u);

wxplot2d(part(%,2), [t,0,1]), v_0 = 10,g=9.8;

18.1. Numerical solution

19. Example 2

Numerical Solutions

From 3Blue1Brown Video | DE1

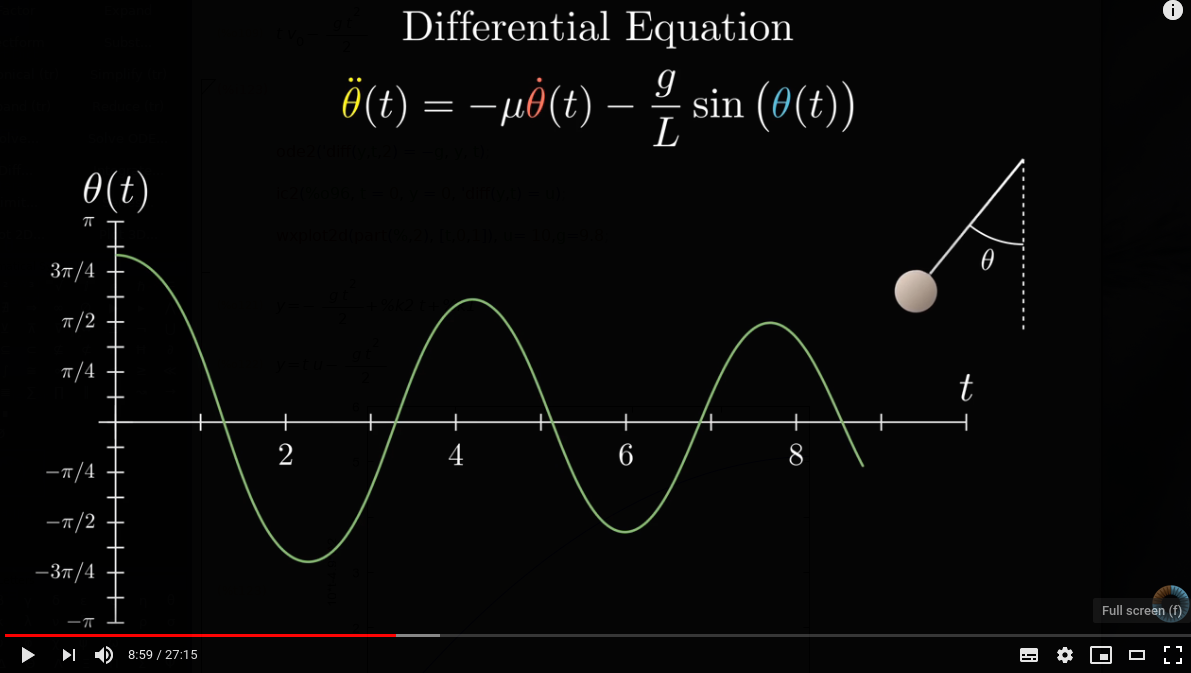
20200907182701-pendulum_equation.png

Figure 4: Pendulum Equation

< Collapse code block> Expand code block 
eqn: 'diff(\theta, t, 2)= - \mu * 'diff(\theta, t) - g/L * sin(\theta);

20. Example 2 (Contd)

Convert second order ode to two first order ode: with independent variables \(\theta\) and \(\omega\) \(\frac{d\theta}{dt} = \omega\) \(\frac {d\omega} {dt} = \alpha = \frac{d^2 \theta}{dt^2} = -\mu \omega - \frac gL \sin(\theta)\)

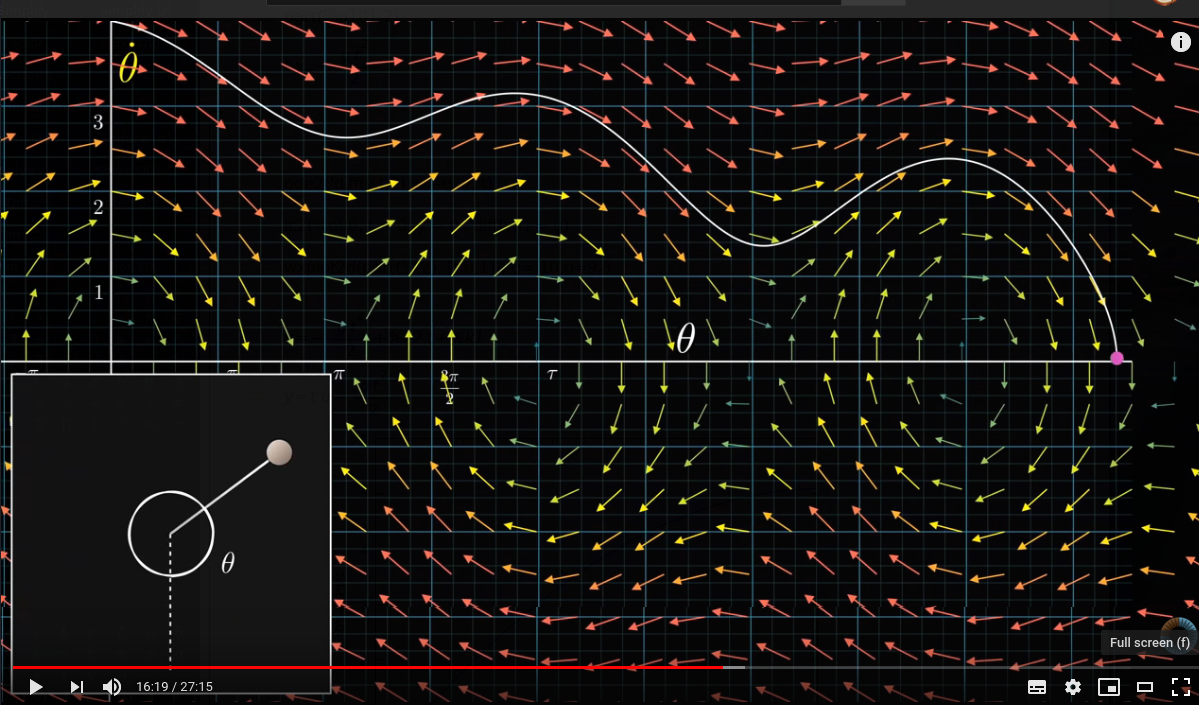
20200907184317-one_intital_condition.png

Figure 5: one intital condition

< Collapse code block> Expand code block 
\alpha:  -\mu * \omega - g / L * sin(\theta);

variables: [\theta, \omega];
derivatives: [\omega, \alpha];

plotdf (derivatives, variables, [parameters, "g=9.81,L=1,mu=0.4"], [\theta, -%pi, 6*%pi], [\omega, -15, 15], [direction, forward], [sliders, "mu=0:2"])$

21. Sums and Products

  • Arithmetic series

  • Geometric series

    < Collapse code block> Expand code block 
    s: sum(1/k^2, k , 1 , inf), simpsum;
tex(s);

    \[{{\pi^2}\over{6}}\]

22. Example : Economics - Linear Gradient Series

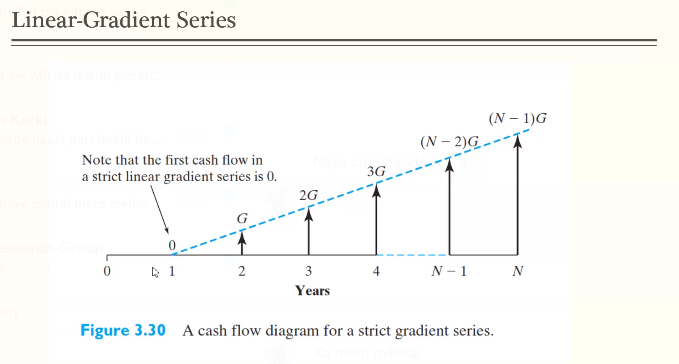
20200904104609-linear_gradient_series.png

< Collapse code block> Expand code block 
P = sum ( G*(y-1)/(1+i)^y, y, 1 ,N);

load("simplifysum")

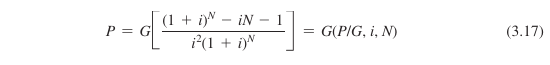
20200907203012-linear_gradient_formula.png

Figure 6: linear gradient formula

23. Example : Economics - Geometric Gradient Series

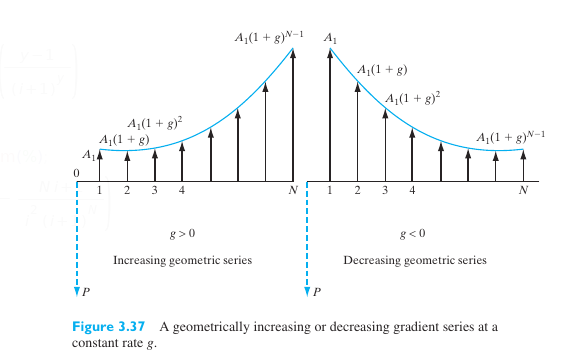
20200907203159-geometric_gradient.png

Figure 8: geometric gradient

< Collapse code block> Expand code block 
P = sum(A_1 * (1+g)^(y-1) / (1+i)^y, y, 1, N);

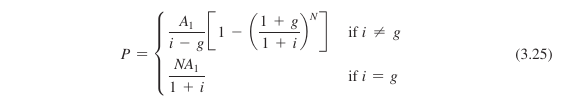
20200907203419-solution.png

Figure 9: solution

24. Other things

  • Taylor expansion
  • List, Matrices, …
  • Functions
  • Control Statements, Loops
  • Laplace Transform

25. Packages

  • Tools not loaded by default
  • Extra tools from users

25.1. Simplex

< Collapse code block> Expand code block 
load("simplex");
maximize_lp(x_1 + 2*x_2, [x_1-x_2 < 5, x_2 < 4]);

26. Mathematica

The BOSS of this field.

20200907141014-some_notable_softwares_mathematica_wolfram_alpha_maple.png

Figure 10: Mathematica

26.1. Try online at

https://www.wolframalpha.com/

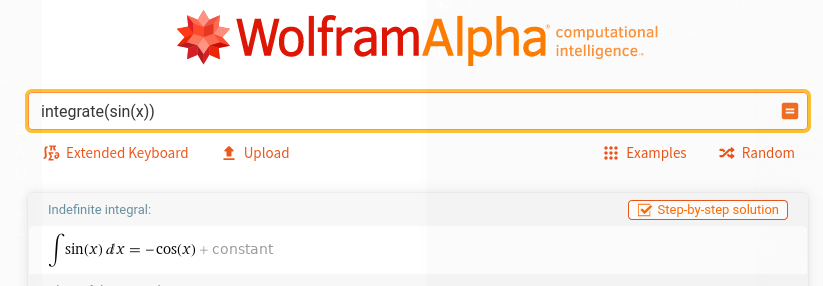
20200907141437-wolfram_alpha.png

Figure 11: Wolfram alpha

27. Maple

20200907141924-maple.png

Figure 12: Maple

20200907211548-popularity_comparision.png (Source)

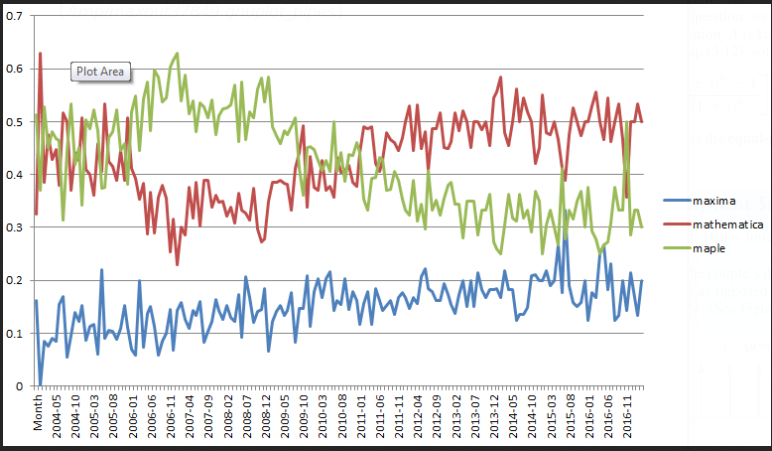
28. Maxima vs ?

Maxima ?
Free expensive
Open Source Proprietary
Powerful Powerful++
Lighweight Heavy
Will Remain Forever Not so sure

Written in Common Lisp.

Install from here. Installation instructions for windows.

29. Bifurcation Diagram / Orbit Diagram

\(x_{n+1} = r x_n (1- x_n)\)

< Collapse code block> Expand code block 
orbits(r*x*(1-x), 0.1, 50, 200, [r,0,4], [style,dots]);

30. I don't know what this is

< Collapse code block> Expand code block 
a1: matrix([0.85,0.04],[-0.04,0.85])$
a2: matrix([0.2,-0.26],[0.23,0.22])$
a3: matrix([-0.15,0.28],[0.26,0.24])$
a4: matrix([0,0],[0,0.16])$
p1: [0,1.6]$
p2: [0,1.6]$
p3: [0,0.44]$
p4: [0,0]$
w: [85,92,99,100]$
ifs(w, [a1,a2,a3,a4], [p1,p2,p3,p4], [5,0], 50000, [style,dots]);

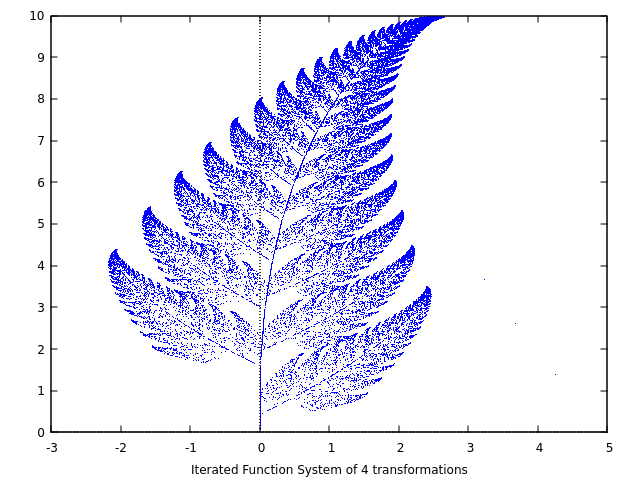
leaf.png

31. Lists & Matrices

[ _ , _ , ….]

append(L, L2) append(L, 3) used to add element to a list

L[i]

length(L)

M : matrix([ ], [ ] , [ ]); invert(M); echelon(M); copymatrix()

Matrix multiplication: M.R

addrow() addcol() ident(n)

M[1,2]

32. Functions

< Collapse code block> Expand code block 
f(x) := x^2;
f(x+1);

33. Control

33.1. IF THEN ELSE

if then else for piecewise function

f(x) := if 0<x and x<1 then x2 else 12

33.2. FOR Loop

m:0; for k:0 thru 100 step 0.5 do m:m+k

33.3. Block

block( m:0, for k:0 thru 100 do m:m+k, m );

s(x) := block( m:0, for k:0 thru s do m:m+k, m );

Backlinks

You can send your feedback, queries here