UP | HOME

Date: <2024-10-02 Wed>

Grokfast

Table of Contents

source: Grokfast - Accelerated Grokking by Ampilfying Slow Gradients - 2405.20233v2.pdf [file:][pdf:][arXiv]

1. Objective

  • to accelerate generalization of a model under grokking phenomenon [pg. 1]
  • x50 improvement (in some cases)

2. Approach

2.1. Parameters as random signals

  • Regard each parameter update as an independent random signal [Page 12]
    • discrete random singal \(u(t) = \theta(t+1) - \theta(t)\)
  • The signal has fast varying (overfitting) and slow varying (generalization) components
  • Represent it in Frequency domain (Fourier transform) [pg. 2]
  • Amplify the low frequency component of the signal

2.2. Gradient correlated with Parameters

  • For first order optimzer gradients are linerly correlated with parameter updates [Page 2]
\begin{align*} x(t) &= Ax(t-1) + Bg(t) \\ u(t) &= Cx(t) + Dg(t) \end{align*}

e.g. Vanilla SGD

\begin{equation*} \theta(t+1) = \theta(t) - \eta g(t) \end{equation*}

2.3. Amplify the low frequency component of \(G(\omega)\)

  • Our hypothesis is that amplifying this low-frequency component of \(G(\omega)\) accelerates the speed of generalization under the grokking phenomenon [pg. 2].

3. Algorithm

3.1. Algorithm - Diagram

[pg. 3]

algorithm_apply_low_pass_filter_on_gradients-20241002072916.png

Figure 1: Algorithm: Apply Low Pass Filter on gradients

3.2. Grokfast-MA (Moving Average)

  • Compute the average gradient in a sliding window (say w=100) (\(g_{avg}\))
  • And add that to the graident \(\hat{g} = g + \lambda g_{avg}\)

Cons:

  • Takes up a lot of memory to store \(w\) copies of gradient
  • Takes longer time to train [pg. 5]

Hyperparameter:

  • w=100 & \(\lambda=5\) worked best [pg. 4]

Result:

  • x14 faster grokking

3.3. Grokfast: Grokfast-EMA (Exponential Moving Average)

  • Compute EMA of the gradient \(\mu = \alpha \mu + (1-\alpha)g\) [pg. 6]
  • Add add that to the gradient \(\hat{g} = g + \lambda \mu\)

Hyperparameters: [pg. 7]

  • \(\lambda \in [0.1, 5]\)
  • \(\alpha \in [0.8, 0.99]\)
  • weight decay (\(w_d\)) dependens on the task
  • Formula might look similar to momentum in optimizers but it is different. [pg. 8]

3.4. Multiple Stages of Learning

[pg. 5]

The model sequentially goes through three distinct stages:

  • (A) initialized, where both training and validation losses are not saturated
  • (B) overfitted, where the training loss is fully saturated but the validation loss is not
  • (C) generalized, where both losses are fully saturated.

Best results found with 2 staged algorithm

  • Don't apply LPF in stage A
  • Apply LPF in stage B, C

Result:

  • Further x1.5 faster groking [pg. 5]

4. Ablation

4.1. Are both slow and fast gradients necessary?

  • Yes
  • Using only the slow gradients calculated from a moving average filter in Algorithm 1 is equivalent to using larger, overlapping minibatches. [pg. 5]
  • Removing original gradient lead to slower and unstable training. [pg. 5]

4.2. Synergy with weight decay

  • When weight decay (wd=0.01) is applied Grokfast-MA got faster by x3.72 [pg. 5]
  • Applying same weight decay without Grokfast-MA makes the training unstable

So, Total speedup is x51 (x14 times x3.7)

5. Experiments

  • MNIST [pg. 7]
    • The handwriting databaset
    • 3 layer ReLU MLP
    • \(\alpha=0.8, \lambda=0.1, w_d = 2\)
    • x22 faster grokking
  • QM9 [pg. 8][PyTorch Geometric]
    • A graph dataset
    • 130,000 molecules with 19 regression targets
    • GCNN
    • \(\alpha=0.8, \lambda=1, w_d = 0.01\)
  • IMDb [pg. 8]
    • Dataset of movie reviews
    • Sentiment analysis
    • 2 layer LSTM
    • \(\alpha=0.98, \lambda=2, w_d = 10\)

6. Visualization Attempt

6.1. Approach

  • See how the parameters move in different stages of training with and without Grokfast
  • Can't visualize all parameters, so take PCA of the parameters [pg. 8]
  • And plot the path as training progresses

(More details in Appendix [pg. 17])

Result:

  • Grokfast pushes to an optimum closer to starting point [pg. 9][pg. 18]
  • Traning is more deterministic under Grokfast [pg. 9]

6.2. Visuals

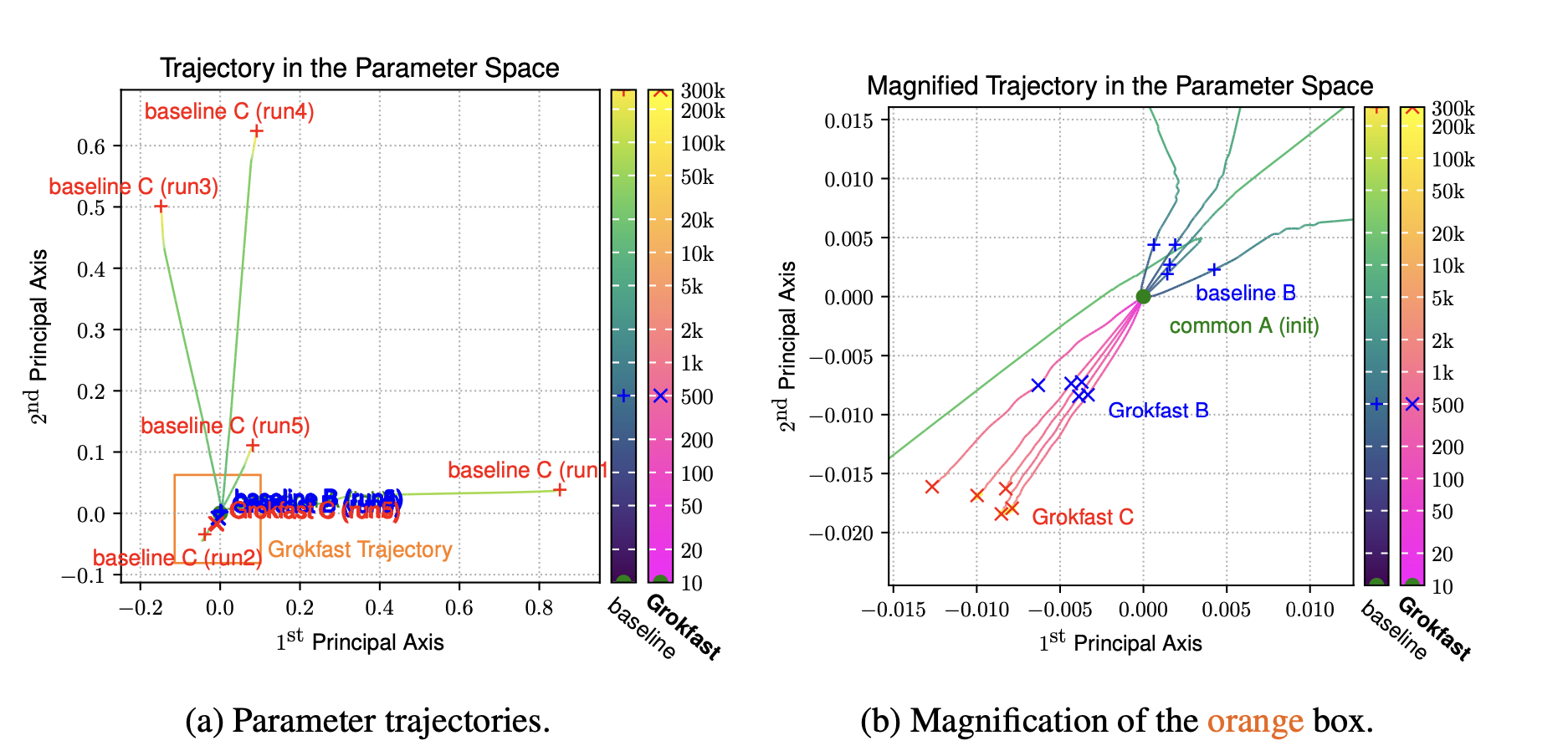
path_in_parameter_space_for-20241002081853.png

Figure 2: Path in Parameter space

7. Misc

  • Nanda et al. [2023] argued that grokking does not occur without proper regularization. [pg. 10]
  • Techniques such as weight decay, L2 norm, and dropout induce grokking, but L1 norm does not [pg. 10]
  • On the other hand, Thilak et al. [2022] argued that grokking can occur without explicit regularization, attributing this to the optimizer’s “visible slingshot mechanism” acting as an implicit regularizer [pg. 10]
You can send your feedback, queries here