Algebraic Structure
Table of Contents
Algebraic Structure consits of
- a nonempty set \(A\),
- a collection of operations on \(A\), and
- a finite set of axioms those operations must satisfy
1. Universal Algebra
Universal algebra (sometimes called general algebra) is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures. For instance, rather than take particular groups as the object of study, in universal algebra one takes the class of groups as an object of study.
1.1. Variety
The collection of all structures of a given type (same operations and same laws) is called a variety in universal algebra. Varieties are restricted to those structures where the axioms can be expressed as identity.
2. Common Axioms
2.1. Equational Axioms
- Commutativity
- Associativity
- Distributivity
- Left Distributivity
- Rigth Distributivity
2.2. Existential Axioms
- Identity
- Inverse
2.3. Non-equational Axioms
Those axioms which can't be expressed as equational or extential axioms. Those structures which have non-equational axioms don't belong to a Variety.
This kind of axioms can be any first-order formula. i.e. contain:
- and, or, not
- \(\forall\), \(\exists\) that apply to elements (not subsets) of the domain of the structure
E.g. Inverse in Fields:
\begin{equation*} \forall x, x = 0 \ or\ x \cdot inv(x) = 1 \end{equation*}Since, inverse is not defined for 0 element of field, inverse in field is a non-equational axioms.
3. Common Algebraic Structures
3.1. 1 Set, No Operation
- Set (Degenerate example of Algebraic Structure)
3.2. 1 Set, 1 binary operation
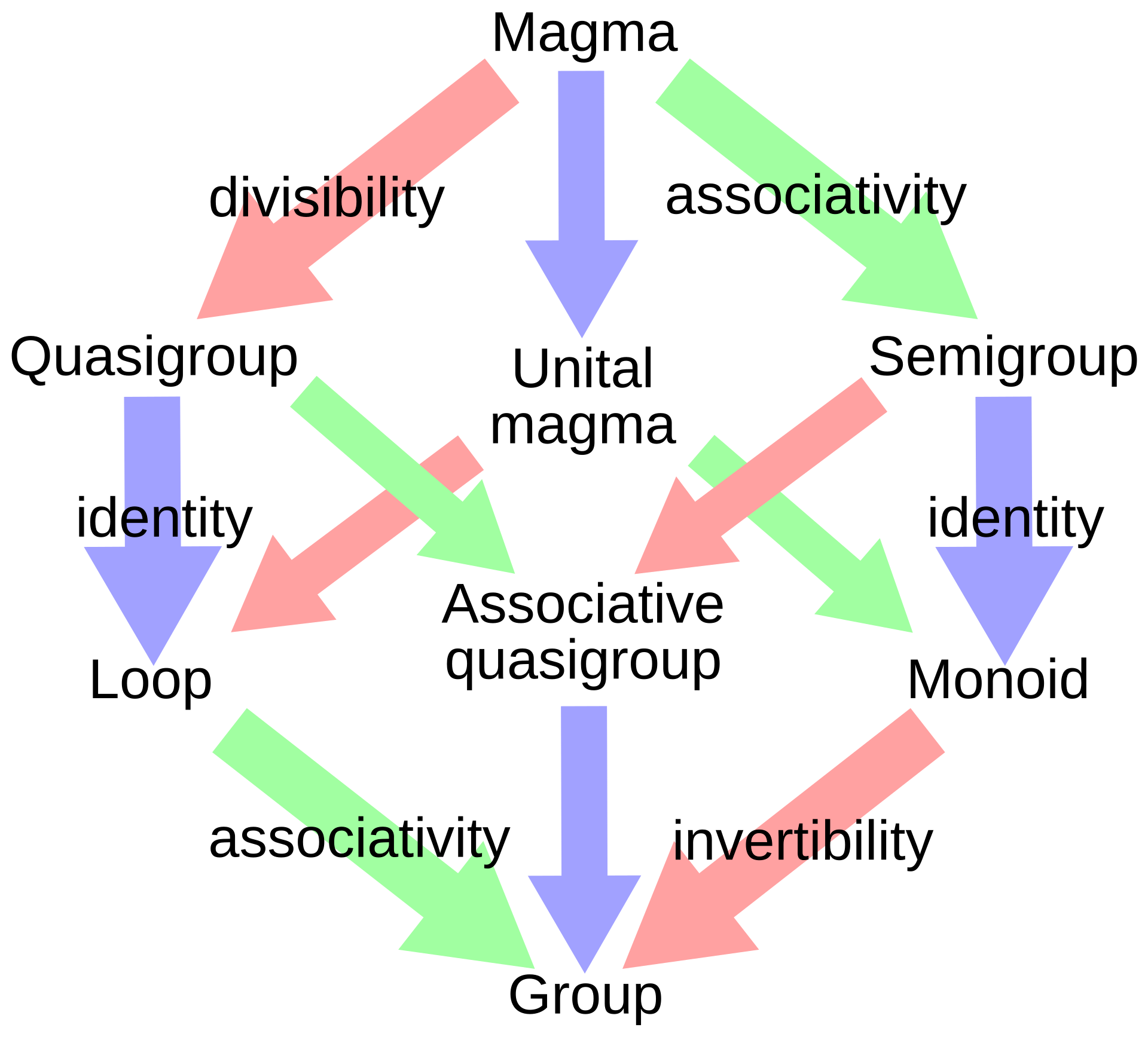
Figure 1: Algebraic Structure between Magma and Group [Source: Wikipedia]
3.3. 1 Set, 2 binary operations
- Ring
- Division Ring
- Commutative Ring
- Field
3.4. 1 set with 2 or more opetaion
- Lattice
- Boolean Algebra
